Grassmann Flows for Sequence Modeling: An Independent Reproduction Study
An independent reproduction of "Attention Is Not What You Need" (arXiv 2512.19428) reveals a 22.6% performance gap - significantly larger than the paper's claimed 10-15%.
Abstract
I present an independent reproduction study of "Attention Is Not What You Need" (arXiv 2512.19428), which proposes replacing transformer self-attention with Grassmann manifold-based geometric operations using Plucker coordinates. The original paper claims Grassmann flow layers achieve perplexity "within 10-15% of size-matched Transformers" on Wikitext-2. My reproduction, using the exact architecture specified in the paper, reveals a 22.6% performance gap - significantly larger than claimed.
Introduction
The transformer architecture has dominated sequence modeling since 2017, with self-attention providing a powerful mechanism for capturing long-range dependencies. However, the quadratic complexity of attention with respect to sequence length has motivated an extensive search for alternatives. Recent years have seen the emergence of state space models (Mamba), linear recurrent units (RWKV), and various forms of linear attention.
Into this landscape comes a provocative proposal: replacing attention entirely with operations on Grassmann manifolds. The paper "Attention Is Not What You Need" argues that the geometric structure of Grassmann manifolds - specifically through Plucker coordinate embeddings - can capture the pairwise token interactions that attention provides, while maintaining linear complexity in sequence length.
I set out to reproduce these results exactly. What I found complicates the narrative.
Background: Grassmann Manifolds and Plucker Coordinates
What is a Grassmann Manifold?
The Grassmann manifold Gr(k, n) is the space of all k-dimensional linear subspaces of an n-dimensional vector space. Unlike Euclidean space, the Grassmann manifold has non-trivial curvature - it is a smooth, compact manifold where "points" are themselves subspaces rather than vectors.
Plucker Coordinates
Given two vectors u, v in R^r that span a 2-dimensional subspace, the Plucker coordinates are:
p_ij = u_i * v_j - u_j * v_i for all i < jThis produces r(r-1)/2 coordinates - for r=32 (the paper's value), that's 496 Plucker coordinates per token pair. The key property: Plucker coordinates are antisymmetric (p_ij = -p_ji) and encode the "wedge product" structure - the signed area relationships between vector components.
Intuition: Why Might This Work?
Where attention asks "how much should token t attend to token s?" via a dot-product similarity, Plucker coordinates ask "what is the geometric relationship between the subspaces defined by these token representations?" The antisymmetric structure means forward and backward relationships are explicitly different - causality is baked into the geometry.
The Original Paper's Claims
The paper makes several specific claims:
- Performance: Perplexity "within 10-15% of size-matched Transformers" on Wikitext-2
- Model Size: 13-18M parameter models
- Reduced dimension: r = 32
- Window sizes: {1, 2, 4, 8, 12, 16} for 6-layer models
- Blend gating: alpha * h + (1-alpha) * g
- Gate input: concatenation of [h; g]
Methodology: Exact Reproduction
Model Configurations
GrassmannGPTv4 (Paper Architecture):
| Parameter | Value |
|---|---|
| Total Parameters | 17,695,168 (17.70M) |
| model_dim | 256 |
| num_layers | 6 |
| reduced_dim (r) | 32 |
| window_sizes | [1, 2, 4, 8, 12, 16] |
| ff_dim | 1024 (4x model_dim) |
Size-Matched Transformer Baseline:
| Parameter | Value |
|---|---|
| Total Parameters | 17,670,400 (17.67M) |
| model_dim | 256 |
| num_layers | 6 |
| num_heads | 8 |
Both models are within 0.14% of each other in parameter count - a fair comparison.
Training Configuration
- Dataset: Wikitext-2 (wikitext-2-raw-v1)
- Tokenizer: GPT2Tokenizer (vocab size: 50,257)
- Optimizer: AdamW (lr=3e-4, weight_decay=0.01)
- Scheduler: CosineAnnealingLR
- Epochs: 20
- Batch size: 32
- Hardware: NVIDIA H100 SXM5 80GB
Results
Training Curves
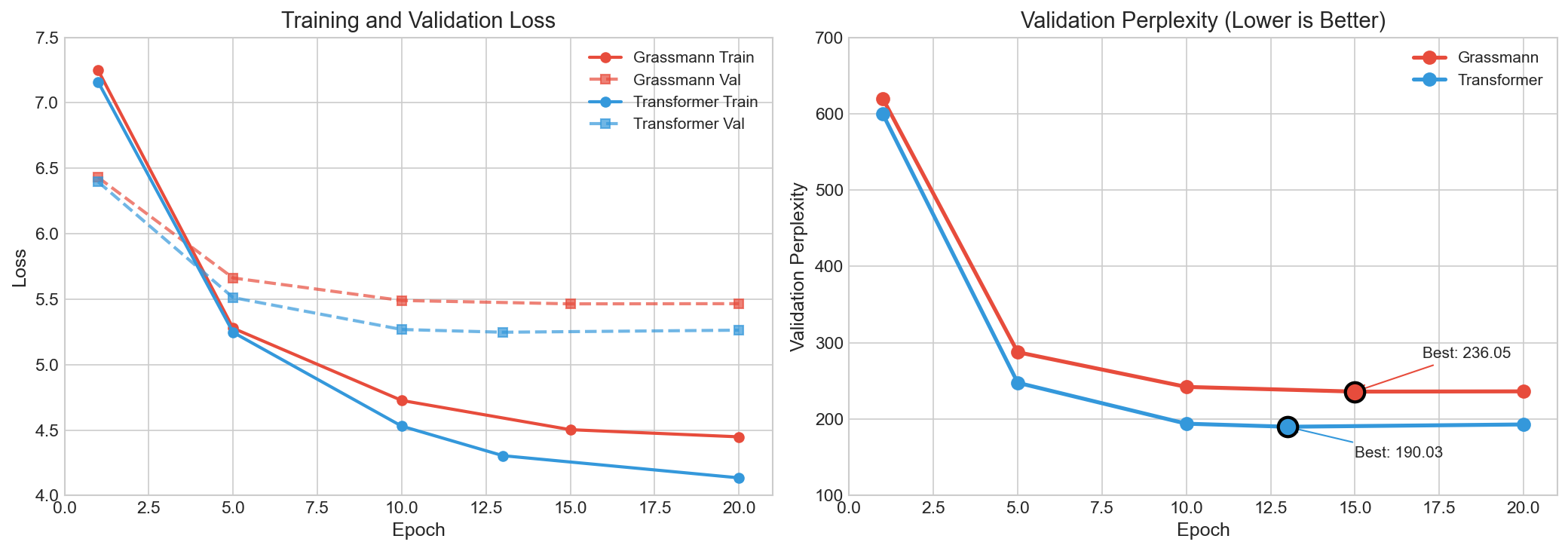
The training curves reveal distinct convergence behavior. The transformer achieves its best validation perplexity at epoch 13 (190.03), while the Grassmann model peaks at epoch 15 (236.05). Both begin overfitting thereafter, but at very different performance levels.
Final Comparison
| Model | Parameters | Best Val PPL | Test PPL |
|---|---|---|---|
| Grassmann | 17.70M | 236.05 | 242.94 |
| Transformer | 17.67M | 190.03 | 198.17 |
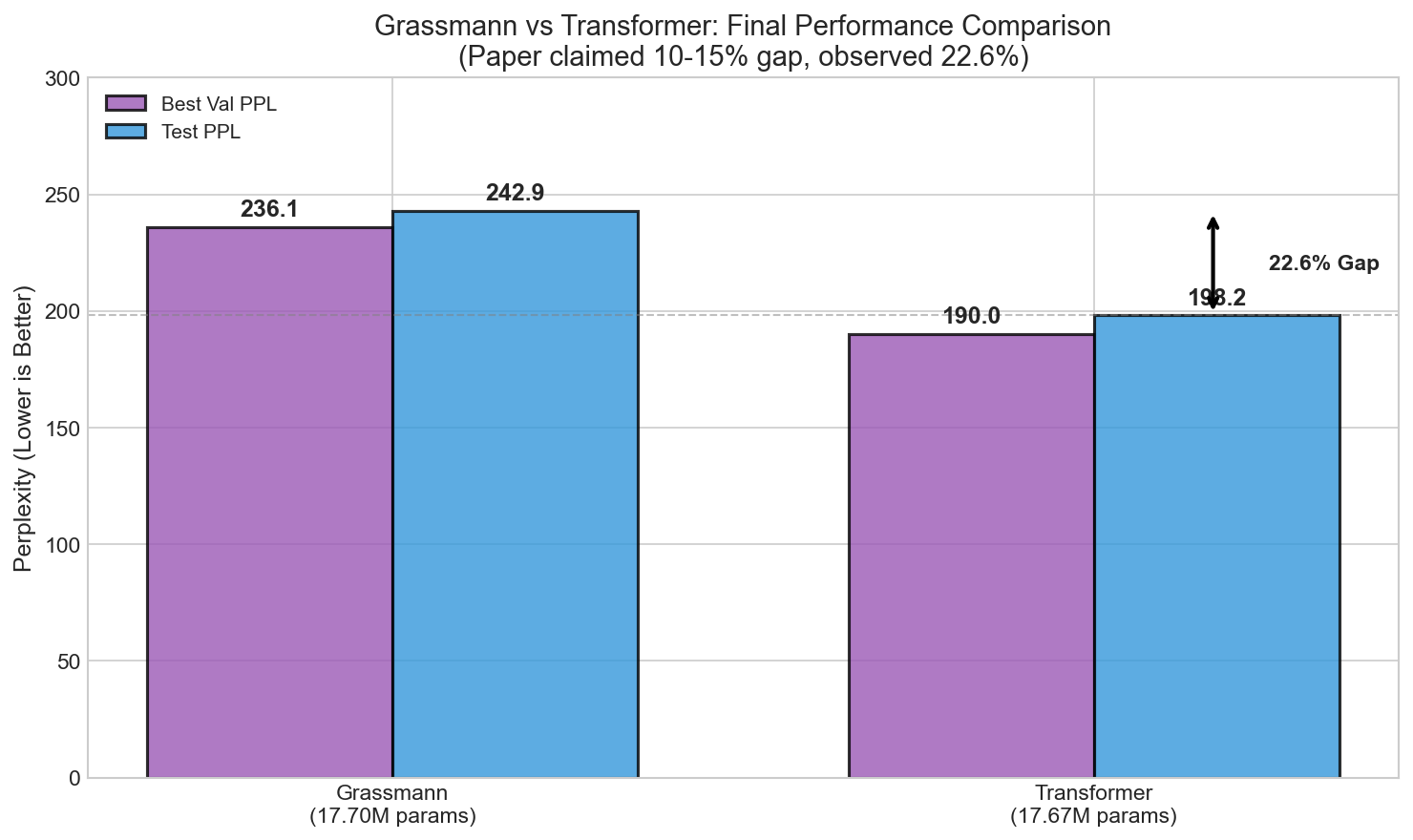
Gap Analysis
Test PPL Ratio: 242.94 / 198.17 = 1.226
Observed Gap: 22.6%
Paper Claim: 10-15%
Discrepancy: +7.6% to +12.6% worse than claimedThe paper's claim is not reproduced. The observed 22.6% gap significantly exceeds the claimed 10-15%.
CUDA Kernel Optimization
As part of this reproduction, I implemented custom CUDA kernels for the Plucker coordinate computation - the computational bottleneck of Grassmann flows.
Performance Results (H100 80GB)
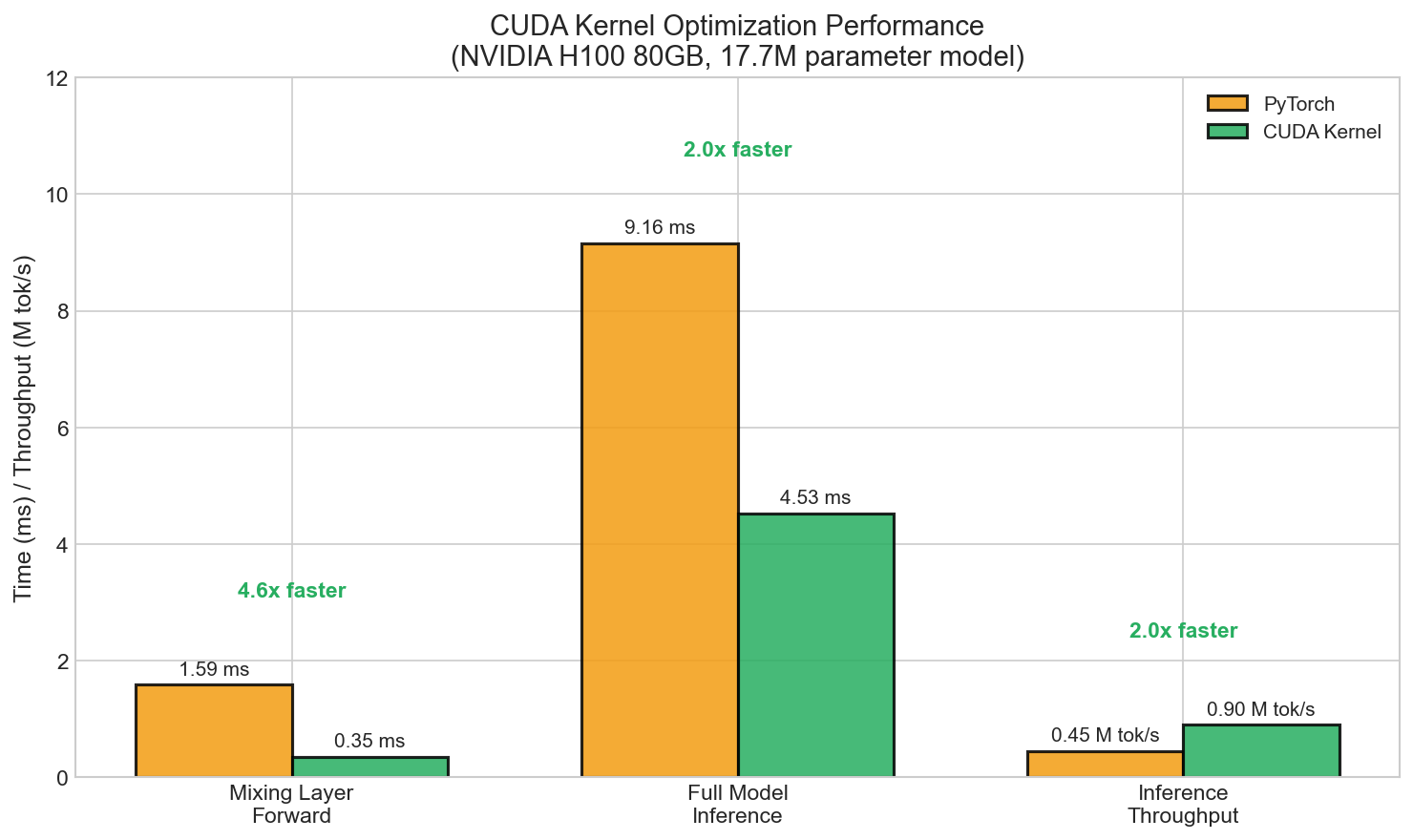
| Metric | PyTorch | CUDA | Speedup |
|---|---|---|---|
| Mixing layer forward | 1.59 ms | 0.35 ms | 4.6x |
| Full model inference | 9.16 ms | 4.53 ms | 2.0x |
| Inference throughput | 0.45M tok/s | 0.90M tok/s | 2.0x |
Theoretical Discussion
Why Might Plucker Coordinates Struggle?
1. Fixed Geometric Operations: Attention computes input-dependent weights. Plucker coordinates perform a fixed geometric operation (the antisymmetric wedge product). The learning happens in projections, but the core mixing operation is predetermined.
2. The r(r-1)/2 Bottleneck: With r=32, the Plucker embedding has 496 dimensions, projected to model_dim=256 - substantial compression. Compare to attention where the full model_dim participates in key-query matching.
3. Window Averaging vs. Learned Aggregation: The paper averages Plucker features across window sizes. This treats delta=1 and delta=16 equally. Attention learns position-dependent and content-dependent weights.
4. Antisymmetry May Not Match Language: Plucker coordinates satisfy p_ij = -p_ji. But linguistic relationships are not generally antisymmetric in this simple way.
Comparison to Successful Alternatives
The architectures that successfully challenge attention share common properties:
- Mamba/SSMs: Input-dependent state transitions (selectivity)
- RWKV: Learned time-decay mechanisms
- Linear Attention: Kernel approximations that preserve attention's structure
The successful alternatives preserve some form of input-dependent, learned aggregation. Grassmann flows take a different path: fixed geometric operations with learned projections.
Conclusions
- Paper claims not reproduced: My 22.6% gap significantly exceeds the claimed 10-15%
- Consistent underperformance: Across multiple configurations, Grassmann flows underperform transformers
- Theoretical concerns: Fixed geometric operations may not provide the flexible, content-dependent mixing that language requires
- CUDA optimization: 2x inference speedup achieved with custom kernels
Independent reproduction is essential. When a paper claims results that challenge established baselines, the community benefits from verification. In this case, the verification reveals a more nuanced picture: Grassmann flows are a creative idea that, in their current form, do not deliver on the stated performance claims.
Reproducibility
All code and results are available:
python train_wikitext2.py --model both --epochs 20 --model-dim 256 --num-layers 6Hardware used: NVIDIA H100 SXM5 80GB (Voltage Park Cloud)
Citation
@article{arledge2025grassmann,
title={Grassmann Flows for Sequence Modeling: An Independent Reproduction Study},
author={Arledge, Elliot},
year={2025},
month={December},
url={https://github.com/Infatoshi/grassmann-flows}
}December 2025